Trigonometric Ratios
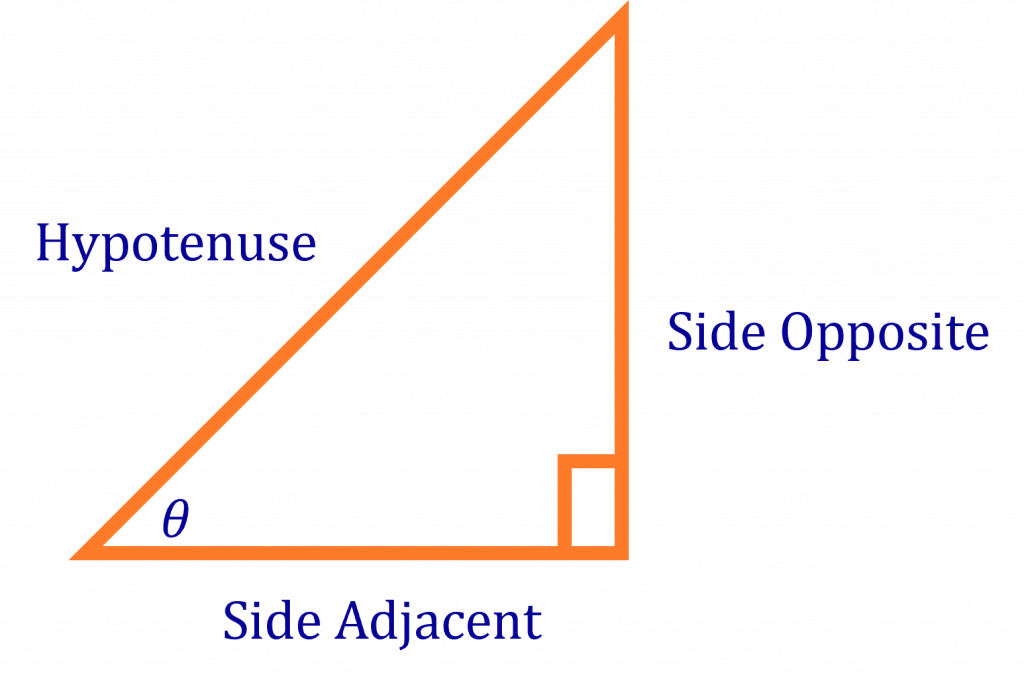
| Function | Abbreviation | Ratio |
| Sine (Sin) | sin (θ) or sin θ | Side Opposite θ / Hypotenuse |
| Cosine (Cos) | cos (θ) or cos θ | Side Adjacent θ / Hypotenuse |
| Tangent (Tan) | tan (θ) or tan θ | Side Opposite θ / Side Adjacent θ |
| Cotangent (Cot) | cot (θ) or cot θ | Side Adjacent θ / Side Opposite θ |
| Secant (Sec) | sec (θ) or sec θ | Hypotenuse / Side Adjacent θ |
| Cosecant (Cosec) | csc (θ) or csc θ | Hypotenuse / Side opposite θ |
Why are trigonometry ratios useful?
Trigonometry ratios are the backbone of countless real-world applications, making them indispensable tools for students, professionals, and enthusiasts alike. These ratios, including Sine, Cosine, Tangent, Cotangent, Secant and Cosecant, enable us to solve complex problems involving angles and distances.
In fields such as engineering, physics, architecture, and astronomy, understanding trigonometry is crucial for designing structures, calculating forces, plotting celestial objects’ paths, and more. Whether you’re a student studying geometry, an engineer designing a bridge, or an architect planning a building’s layout, mastering trigonometry ratios unlocks a world of possibilities for precise measurements, calculations, and problem-solving.
Where can I find out more about about trigonometry ratios?
For additional information and an in-depth explanation on trigonometry and the trigonometric ratios, please refer to the following Wikipedia reference.